AGD Modules ( AGDModule )

Baseclasses

Definition

The class AGDModule is the base class for modules in the AGD-Library. It provides the handling of pre- and postconditions, and defines a uniform access to common informations about a module.

The Type of a Module

We can characterize the type of a module by defining the type of its input I₁,..., I_n, the type of its output O₁,..., O_m, and the associated functionality, e.g., augmentation or layout algorithm. We express the different types of modules by abstract base classes derived from AGDModule, which define the input and output types, and the functionality.

The input consists of n $\geq$ 0 and the output of m $\geq$ 0 parameters of an arbitrary abstract (not necessarily C++) type. The call() method of a particular module uses appropriate classes to represent these types. It is not necessary to represent each abstract type by exactly one class, for example

• the type ``grid layout'' can be represented by ``node_map<int>& x, node_map<int>& y, edge_map<IPolyline>& bends'',
• an input and output parameter ``graph'' can be represented by a single graph reference.

Precondition and Postcondition

AGDModule maintains a set pre(i) of properties for each input parameter I_i, 1 < = i < = n, which must be satisfied by I_i if the module is called. Properties are expressed by key items (cf. Sect. AGD Base), and sets of properties by the data type KeySet. We call pre(i) the precondition of I_i, and pre(1),..., pre(n) the precondition of the module.

The postcondition of the output parameters are sets of properties that the output will always satisfy. We allow that they depend on the properties P₁,..., P_n that the input of the module satisfies. Clearly, these properties must be more general than the required precondition, i.e., P_i $\supseteq$ pre(i) must hold for all 1 < = i < = n. We associate a function post(i) : $\protectP$(KEYS)ⁿ$\to$$\protectP$(KEYS) with each output parameter O_i, where KEYS is the set of all properties. We also reserve a special postcondition with index 0 for general properties of the module.

The function post(i) is defined by a set of rules post_rules(i), where each rule is of the form

$(p_1,i_1) \wedge \ldots \wedge (p_k,i_k) \rightarrow p\mbox{ , }k>= 0.$
Such a rule means that if, for each 1 < = j < = k, input parameter I_ij satisfies property p_j, then output parameter O_i satisfies property p.

AGDModule provides protected methods to insert rules into post_rules(i), and to remove rules from post_rules(i). Rules in post_rules(i) can be accessed via the item type pr_item, e.g., to remove a rule. The function defined by post_rules(i) is given by

$$\begin{eqnarray*} \lefteqn{\HTML{I}{post}(\HTML{I}{i})(Q_1,\ldots,Q_n) =} \\ & ... ...st\_rules}(i)\mbox{ with } p_j\in Q_{i_j}\forall 1\leq j\leq k\} \end{eqnarray*}$$

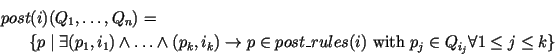
Note, that the so defined functions are monotonous in the following way. If P_j $\subseteq$ Q_j holds for all 1 < = j < = n, then post(i)(P₁,..., P_n) $\subseteq$ post(i)(Q₁,..., Q_n) holds for each 1 < = i < = m.

We represent a precondition P₁,..., P_n by the data type PreCond, a postcondition Q₀,..., Q_m by the data type PostCond, and a postcondition rule R₀,..., R_m by the data type PostCondRule, where P_i, Q_i are sets of keys and R_i are sets of rules.

Common Informations

Every AGD module contains

• a name in a long (long_name) and a short (name) version.
• an author (author).
• the name of the author (impl_author), the version (impl_version), and the date (impl_date) of the implementation.

The default implementations for name(), author(), impl_author(), impl_version() and impl_date() return an empty string ``'' indicating that this information is unknown. long_name() returns name() by default.

Exchangeable Modules and Optional Parameters

We recommend to provide a standard interface for exchangeable modules and optional parameters. These recommendation is obeyed by the module implementations in the library.

Exchangeable modules are implemented as module options (see Sect. Module Options) with an additional method set_name(type M), which sets the module option name to M if possible.

An optional parameter name of type type provides two methods

void	name( type new_setting)
type	name()

for setting and reading the current value of the option. The documentation describes optional parameters in the definition section of its class in the following way

• type name = initial_value
  description

where initial_value is the default setting of the option.

#include < AGDModule.h >

Initialization

AGDModule

M(int n, int m)

initializes a module with n input and m output parameters. Initializes pre(i) and post(j) with the empty set for all 1 < = i < = n, and 0 < = j < = m.

Operations

a) Queries on Preconditions and Postconditions

int	M.num_in_param()	returns the number of input parameters n.
int	M.num_out_param()	returns the number of output parameters m.
const PreCond&	M.precondition()	returns pre.
const KeySet&	M.precondition(int i)	returns pre(i). Precondition: 1 < = i < = n.
PostCond	M.postcondition(const PreCond& PRE)
		returns post(pre(1),..., pre(n)).
const KeySet&	M.postcondition(int i = 1)
		returns post(i)(pre(1),..., pre(n)). Precondition: 0 < = i < = m.
KeySet	M.postcondition(const PreCond& PRE, int i)
		returns post(i)(PRE). Precondition: 0 < = i < = m, and PRE.num_param() = n.
bool	M.applicable(const PreCond& PRE, const PostCond& POST)
		returns true iff M can be applied as module for guaranteed precondition PRE and required postcondition POST, i.e., PREi $\supseteq$ pre(i) $\forall$ 1 < = i < = n and post(j)(PRE) $\subseteq$ POSTj $\forall$ 0 < = j < = m.
AGDModule *	M.clone()	returns a pointer to a new instance with the same option settings as M. Must be overridden by module implementations.

b) General Information

leda_string	M.name()	returns the name of the algorithm.
leda_string	M.long_name()	returns the name in an extended version.
leda_string	M.author()	returns the author of the algorithm.
leda_string	M.impl_author()	returns the author of the implementation.
leda_string	M.impl_version()	returns the version of the implementation.
leda_string	M.impl_date()	returns the date of the last change of the implementation.

c) Protected Methods for Maintaining Preconditions

void	M.add_precondition(AgdKey k, int i = 1)
		adds the key k to pre(i). Precondition: 1 < = i < = n.
void	M.add_precondition(AgdKey k, bool status, int i = 1)
		adds the key k to pre(i) if status = true, removes it otherwise. Precondition: 1 < = i < = n.
void	M.add_preconditions(const leda_string& ps, char delim = ', ', int i = 1)
		interprets ps as a list of strings seperated by delim, and adds the key for each string to pre(i). Precondition: 1 < = i < = n.
void	M.rem_precondition(AgdKey k, int i = 1)
		removes the key k from pre(i). Precondition: 1 < = i < = n.

d) Protected Methods for Maintaining Postconditions

pr_item	M.add_post_rule(AgdKey k, int i = 1)
		adds a new rule item < $\rightarrow$ k > to post_rules(i) and returns it. Precondition: 0 < = i < = m.
pr_item	M.add_post_rule(AgdKey p1, int i1, AgdKey p, int i = 1)
		adds a new rule item < (p1, i1) $\rightarrow$ p > to post_rules(i) and returns it. Precondition: 0 < = i < = m.
pr_item	M.add_post_rule(const TaggedRule& r, int i = 1)
		adds a new rule item < r > to post_rules(i) and returns it. Precondition: 0 < = i < = m.
void	M.rem_post_rule(pr_item it, int i = 1)
		removes the rule item it from post_rules(i). Precondition: 0 < = i < = m and it is a rule item in post_rules(i).

Checking the Precondition of a Module

Particular module types, for example LayoutModule, provide a method check() that checks if a given input satisfies the precondition of the module. AGDModule implements extendable default implementations to check a precondition for specific types, for example graphs. These default implementations can be used by the base class of a particular module type (e.g., LayoutModule) to implement its check() method.

The method check_graph() can test if a given input graph satisfies the following keys: directed, undirected, planar, simple, no_self_loops, no_reversals, connected, biconnected, triconnected, bipartite, four_graph, acyclic, forest, tree, single_source, single_sink. If check_graph() finds another key it calls check_graph_key().

bool	M.check_graph(int i, const leda_graph& G, AgdKey& p)
		returns true if G satisfies the preconditions pre(i). Otherwise, false is returned, and p contains a property that is not satisfied.
bool	M.check_graph_key(AgdKey p, const leda_graph& G)
		overridable to extend check_graph. Must return true if G satisfies p, false otherwise. The default implementation returns false.
bool	M.check_graph(int i, const ClusterGraph& CG, AgdKey& p)
		returns true if CG satisfies the preconditions pre(i). Otherwise, false is returned, and p contains a property that is not satisfied.
bool	M.check_graph_key(AgdKey p, const ClusterGraph& CG)
		overridable to extend check_graph. Must return true if CG satisfies p, false otherwise. The default implementation returns false.