Mapping with Adjusted Grid Width ( MaxEachMapper )

Baseclasses

Definition

MaxEachMapper provides a mapping, which tries to reduce the width and height of the resulting layout, such that the distance between two nodes is at least sep_x in x-direction and sep_y in y-direction.

The input grid sizes of nodes ( get_node_gride_size() function) are

$$\begin{eqnarray*} \HTML{I}{grid\_width}(v) & = & \max\left( 0,\left\lceil \frac{... ...}(v)+\HTML{I}{sep\_y}} {\HTML{I}{width\_y}}-1\right\rceil\right) \end{eqnarray*}$$

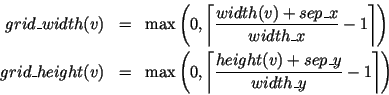
Let wc(x) be the width of column x and wr(y) the width of row y. MaxEachMapper computes a (not necessarily optimal) solution of the two optimization problems

min$\sum\limits_{x=xmin}^{xmax}$wc(x) s.t.
	wc(x)	> =	2min$\_$over$\_$x + sep$\_$x	for all xmin < = x < = xmax
	$\sum\limits_{i=xl}^{xr}$wc(i)	> =	width(v) + sep$\_$x	for all v $\in$ V, xl = column(v), xr = xl + grid$\_$width(v)

and

min$\sum\limits_{y=ymin}^{ymax}$wr(y) s.t.
	wr(y)	> =	2min$\_$over$\_$y + sep$\_$y	for all ymin < = y < = ymax
	$\sum\limits_{i=yb}^{yt}$wr(i)	> =	height(v) + sep$\_$y	for all v $\in$ V, yb = row(v), yt = yb + grid$\_$height(v)

The width of node v is eventually enlarged, such that it is at least

$\left\{\begin{array}{cl} 2\HTML{I}{min\_over\_x} & \mbox{if }\HTML{I}{xl}=\HTML... ...I}{xl})+\HTML{I}{wc}(\HTML{I}{xr})\right) & \mbox{otherwise} \end{array}\right.$
where xl = column(v) and xr = xl + grid$\_$width(v), and the height such that it is at least

$\left\{\begin{array}{cl} 2\HTML{I}{min\_over\_y} & \mbox{if }\HTML{I}{yb}=\HTML... ...I}{yb})+\HTML{I}{wr}(\HTML{I}{yt})\right) & \mbox{otherwise} \end{array}\right.$
where yb = row(v) and yt = yb + grid$\_$height(v).

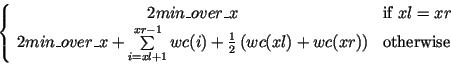
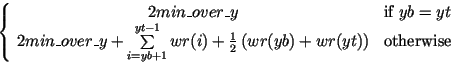
The realized mapping is defined as

$$\begin{eqnarray*} \varphi_x(i) & = & \HTML{I}{origin}.\HTML{I}{x} + \sum\limits_... ...c{1}{2}\left(\HTML{I}{wr}(\HTML{I}{ymin})+\HTML{I}{wr}(i)\right) \end{eqnarray*}$$

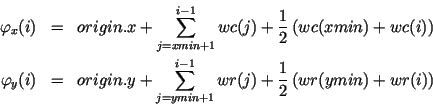
Optional Parameters Instances of MaxEachMapper provide the following optional parameters:

$\bullet$

double width_x = 40
determines the grid width in x-direction used by get_node_grid_size() in order to determine the grid size of nodes.

$\bullet$

double width_y = 40
determines the grid width in y-direction used by get_node_grid_size().

$\bullet$

double min_overhang_x = 2
determines the minimal allowed overhang of each node in x-direction.

$\bullet$

double min_overhang_y = 2
determines the minimal allowed overhang of each node in y-direction.

$\bullet$

double sep_x = 20
determines the minimal distance (separation) between nodes in x-direction.

$\bullet$

double sep_y = 20
determines the minimal distance between nodes in y-direction.

$\bullet$

DPoint origin = (0, 0)
determines the origin of the coordinate system, that is the point to which the lower left grid point (xmin, ymin) is mapped.

#include < AGD/MaxEachMapper.h >

Creation

MaxEachMapper	M(double width_x = 40, double width_y = 40, double min_overhang_x = 2, double min_overhang_y = 2, double sep_x = 20, double sep_y = 20, DPoint origin = DPoint(0, 0))
		creates an instance M of type MaxEachMapper, and sets the optional parameters width_x, width_y, min_overhang_x, min_overhang_y, sep_x, sep_y and origin.

Operations

Standard Interface (Inherited Methods) The detailed description of these methods can be found in the manual entries of the base class (GridCoordinateMapper).

void	M.get_node_grid_size(const leda_graph& G, GridLayout& gl, const LayoutInterface& A)
void	M.get_node_grid_size(const GraphCopy& GC, GridLayout& gl, const LayoutInterface& A)
void	M.call(const leda_graph& G, const GridLayout& gl, LayoutInterface& A)
void	M.call(const GraphCopy& GC, const GridLayout& gl, LayoutInterface& A)

Access to Options

double	M.width_x()
void	M.width_x(double wx)
double	M.width_y()
void	M.width_y(double wy)
double	M.min_overhang_x()
void	M.min_overhang_x(double x)
double	M.min_overhang_y()
void	M.min_overhang_y(double y)
double	M.sep_x()
void	M.sep_x(double x)
double	M.sep_y()
void	M.sep_y(double y)
DPoint	M.origin()
void	M.origin(DPoint p)

Implementation

Let n be the number of nodes and m the number of edges in G, b the total number of bend points, s the number of rows and columns in the grid layout, and denote with gc(v) the number of columns and with gr(v) the number of rows covered by rect(v). Then, get_node_grid_size() takes time $\protectO$(n) and call() takes time

$\protectO \left( s+n+m+b+ \sum_{v\in V} \left( 1+\mathit{gc}(v)\log \mathit{gc}(v)+\mathit{gr}(v)\log \mathit{gr}(v)\right) \right).$