Optimal Layout of Hierarchies ( OptCompCoord )

Baseclasses

Definition

The class OptCompCoord represents a layout algorithm for hierarchies which assigns x-coordinates to nodes according to the optimal solution of an optimization problem. The y-coordinates are computed in a straight-forward way.

More precisely, the optimization problem is defined as follows

min$\sum\limits_{(u,v)\in E}^{}$$\Omega$(u, v) x(u) - x(v) s.t.
	x(v) - x(u)	> =	$\frac{1}{2}(\HTML{I}{width}(v)+\HTML{I}{width}(u)) + \HTML{I}{node\_distance}$	where v is successor of u on the same layer
	x(v)	> =	origin.y	for all v $\in$ V

where the hierarchy represents the graph G = (V, E). The aim of the objective function is to make edges run as vertically as possible. For each edge e, $\Omega$(e) defines the weight of e in the objective function. We distinguish three cases:

$\Omega(e) = \left\{ \begin{array}{cl} \HTML{I}{weight0} & \mbox{no endpoint of... ...ht2} & \mbox{both endpoints of }e\mbox{ are dummy vertices} \end{array} \right.$
The values of weight0, weight1 and weight2 are optional parameters. The default settings are 1, 2 and 8, respectively, what gives edges with to adjacent dummy vertices the heaviest weight because these edges represent interior segments of long edges in the actual graph.

The y-coordinates of the layers L₁,..., L_n are defined recursively:

$$\begin{eqnarray*} y(L_n) & = & \HTML{I}{origin}.\HTML{I}{y}\\ y(L_i) & = & y(L_... ...}{2}(h_i+h_{i+1}) + \HTML{I}{layer\_distance}\quad\mbox{for }i<n \end{eqnarray*}$$

where h_i denotes max{height(v) | v $\in$ L_i}.

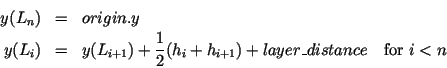
General Information

Algorithm
name	OptCompCoord
long name	Optimal Layout of Hierarchies
author

Implementation
author	C. Gutwenger
date	June 1999
version	1.0

Pre- and Postcondition

precondition	=	$\emptyset$
postcondition(PRE)	=	$\emptyset$

Optional Parameters Instances of OptCompCoord provide the following optional parameters:

$\bullet$

double node_distance = 3.0
defines the minimal horizontal distance between two nodes on the same layer.

$\bullet$

double layer_distance = 3.0
defines the minimal vertical distance between two nodes on neighbored layers.

$\bullet$

DPoint origin = (0.0, 0.0)
defines the y-coordinate of the lowest layer and the smallest possible x-coordinate of a vertex.

$\bullet$

double weight0 = 1.0
defines the weight of edges which are not adjacent to a dummy vertex.

$\bullet$

double weight1 = 2.0
defines the weight of edges which are adjacent to exactly one dummy vertex.

$\bullet$

double weight2 = 8.0
defines the weight of edges which are adjacent to two dummy vertices.

#include < AGD/OptCompCoord.h >

Creation

OptCompCoord

L

creates an instance L of type OptCompCoord.

Operations

Standard Interface (Inherited Methods) The detailed description of these methods can be found in the manual entries of the base class (HierarchyLayoutModule).

bool	L.check(const GraphCopy& GC, const Hierarchy& H, AgdKey& p)
void	L.call(const GraphCopy& GC, const Hierarchy& H, LayoutInterface& A)

Access to Options

double	L.node_distance()
void	L.node_distance(double x)
double	L.layer_distance()
void	L.layer_distance(double x)
DPoint	L.origin()
void	L.origin(DPoint p)
double	L.weight0()
void	L.weight0(double x)
double	L.weight1()
void	L.weight1(double x)
double	L.weight2()
void	L.weight2(double x)

Implementation

The optimization problem is refomulated as a linear program, which is solved with an LP-solver.