




Next: The Canonical Ordering of
Up: Canonical Orderings
Previous: Canonical Orderings
Contents
Index
Sets of a Canonical Ordering ( OrderSet )
Definition
An instance V of type OrderSet represents one set of a canonical
ordering C of a graph G = (V, E). It contains a set
{v,..., vp} of
nodes of G ordered from left to right, a leftvertex c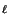 , a
rightvertex cr, and additional information has_left
and has_right, where
has
, a
rightvertex cr, and additional information has_left
and has_right, where
has left = true
left = true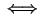 (v1, c
(v1, c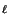 )
) 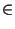 E,
and
has
E,
and
has right = true
right = true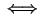 (vp, cr)
(vp, cr) 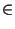 E.
E.
#include < AGD/CanonicalOrder.h >
Creation
| OrderSet |
V |
creates an instance V of type OrderSet representing
an empty set.
|
| OrderSet |
V(int l, leda_edge el = nil, leda_edge er = nil) |
| |
|
creates an instance V of type OrderSet representing
a set of length l with left edge el and right edge er.
|
Operations
| leda_node |
V.left() |
returns the leftvertex c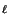 of V. of V.
|
| leda_node |
V.right() |
returns the rightvertex cr of V.
|
| leda_edge |
V.left_edge() |
returns the edge
(z1, c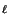 ) or nil. ) or nil.
|
| leda_edge |
V.right_edge() |
returns the edge (zp, cr) or nil.
|
| bool |
V.has_left() |
returns the information has_left of V.
|
| bool |
V.has_right() |
returns the information has_right of V.
|
| void |
V.left(leda_node cl) |
sets the leftvertex of V to cl.
|
| void |
V.right(leda_node cr) |
sets the rightvertex of V to cr.
|
| void |
V.left_edge(leda_edge el) |
sets the edge
(z1, c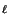 ). ).
|
| void |
V.right_edge(leda_edge er) |
| |
|
sets the edge (zp, cr).
|
| int |
V.len() |
returns the length of V, i.e. the number of nodes in
V.
|
| leda_node& |
V[const int i] |
returns the i-th node of V from left (the leftmost
node has index 1).
|
Implementation
Order sets are implemented by arrays. All operations take constant time.





Next: The Canonical Ordering of
Up: Canonical Orderings
Previous: Canonical Orderings
Contents
Index
© Copyright 1998-2001, Algorithmic Solutions Software GmbH. All rights reserved.
2001-08-13





![]() , a
rightvertex cr, and additional information has_left
and has_right, where
has
, a
rightvertex cr, and additional information has_left
and has_right, where
has![]() left = true
left = true![]() (v1, c
(v1, c![]() )
) ![]() E,
and
has
E,
and
has![]() right = true
right = true![]() (vp, cr)
(vp, cr) ![]() E.
E.




