




Next: Skeletons ( Skeleton )
Up: SPQR-Trees
Previous: SPQR-Trees ( SPQRTree )
Contents
Index
SPQR-Trees for Planar Graphs ( PlanarSPQRTree )
Baseclasses

Definition
The class PlanarSPQRTree maintains the triconnected components of a
planar biconnected graph G and represents all possible embeddings
of G. Each skeleton graph is embedded, i.e., it is a planar map.
The current embeddings of the skeletons define an embedding of G.
There are two basic operations for obtaining another embedding
of G: reverse(v), which flips the skeleton of an R-node v
around its poles, and swap
(v, e1, e2), which exchanges the
positions of the edges e1 and e2 in the skeleton of a
P-node v.
#include < AGD/PlanarSPQRTree.h >
Creation
| PlanarSPQRTree |
T(const leda_graph& G, bool is_planar_map = false) |
| |
|
creates an SPQR tree
 for planar graph G rooted at
the first edge of G. If is_planar_map is set to true, G must be a
planar map, i.e., for each edge e the reversal information rev(e)
is set and the counter-clockwise order of the outgoing edges of each
vertex defines an embedding. In this case, e and rev(e) are considered as a single
edge. Precondition: G is planar and biconnected and contains at least 3 nodes,
or G has exactly 2 nodes and at least 3 (resp. 6 if is_planar_map
is true) edges. for planar graph G rooted at
the first edge of G. If is_planar_map is set to true, G must be a
planar map, i.e., for each edge e the reversal information rev(e)
is set and the counter-clockwise order of the outgoing edges of each
vertex defines an embedding. In this case, e and rev(e) are considered as a single
edge. Precondition: G is planar and biconnected and contains at least 3 nodes,
or G has exactly 2 nodes and at least 3 (resp. 6 if is_planar_map
is true) edges.
|
| PlanarSPQRTree |
T(const leda_graph& G, leda_edge e, bool is_planar_map = false) |
| |
|
creates an SPQR tree
 for planar graph G rooted at edge e.
If is_planar_map is set to true, G must be a
planar map, i.e., for each edge e the reversal information rev(e)
is set and the counter-clockwise order of the outgoing edges of each
vertex defines an embedding. In this case, e and rev(e) are considered as a single
edge. Precondition: G is planar and biconnected and contains at least 3 nodes,
or G has exactly 2 nodes and at least 3 (resp. 6 if is_planar_map
is true) edges. for planar graph G rooted at edge e.
If is_planar_map is set to true, G must be a
planar map, i.e., for each edge e the reversal information rev(e)
is set and the counter-clockwise order of the outgoing edges of each
vertex defines an embedding. In this case, e and rev(e) are considered as a single
edge. Precondition: G is planar and biconnected and contains at least 3 nodes,
or G has exactly 2 nodes and at least 3 (resp. 6 if is_planar_map
is true) edges.
|
Operations
| leda_integer |
T.number_of_embeddings() |
returns the number of possible embeddings of G.
|
| leda_integer |
T.number_of_embeddings(leda_node v) |
| |
|
returns the number of possible embeddings of the pertinent
graph of node v. Precondition:
v 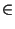 
|
| void |
T.reverse(leda_node v) |
flips the skeleton S of v around its poles by reversing
the order of outgoing edges of each vertex in S. Precondition: v
is an R-node in  . .
|
| void |
T.swap(leda_node v, leda_edge e1, leda_edge e2) |
| |
|
exchanges the positions of e1 and e2 in skeleton of v.
Precondition: v is a P-node in  and
e1, e2 and
e1, e2 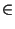 skeleton(v). skeleton(v).
|
| void |
T.embed(leda_graph& G) |
embeds G according to the current embeddings of the skeletons
of  . Precondition: G is the graph passed to the constructor of . Precondition: G is the graph passed to the constructor of  and G is a map.
and G is a map.
|
| void |
T.random_embed() |
embeds all skeleton graphs randomly.
|
| void |
T.random_embed(leda_graph& G) |
| |
|
embeds all skeleton graphs randomly, and embeds G according to
the embeddings of the skeletons. Precondition: G is the graph passed to
the constructor of  and G is a map. and G is a map.
|
Implementation
Let n be the number of vertices and m be the number of edges in
G. The construction of an SPQR-tree  for graph G
takes time
for graph G
takes time
 (n + m). Operations embed() and random_embed()
take time
(n + m). Operations embed() and random_embed()
take time
 (n + m), reverse(v) takes time
(n + m), reverse(v) takes time
 (| skeleton(v)|), and swap() takes constant time.
Operation number_of_embeddings() takes time
(| skeleton(v)|), and swap() takes constant time.
Operation number_of_embeddings() takes time
 (n + m) and
number_of_embeddings(vT) takes time
(n + m) and
number_of_embeddings(vT) takes time
 (| P|),
where P is the pertinent graph of vT.
The data structure uses
(| P|),
where P is the pertinent graph of vT.
The data structure uses
 (n + m) space.
(n + m) space.





Next: Skeletons ( Skeleton )
Up: SPQR-Trees
Previous: SPQR-Trees ( SPQRTree )
Contents
Index
© Copyright 1998-2001, Algorithmic Solutions Software GmbH. All rights reserved.
2001-08-13







![]() for graph G
takes time
for graph G
takes time
![]() (n + m). Operations embed() and random_embed()
take time
(n + m). Operations embed() and random_embed()
take time
![]() (n + m), reverse(v) takes time
(n + m), reverse(v) takes time
![]() (| skeleton(v)|), and swap() takes constant time.
Operation number_of_embeddings() takes time
(| skeleton(v)|), and swap() takes constant time.
Operation number_of_embeddings() takes time
![]() (n + m) and
number_of_embeddings(vT) takes time
(n + m) and
number_of_embeddings(vT) takes time
![]() (| P|),
where P is the pertinent graph of vT.
The data structure uses
(| P|),
where P is the pertinent graph of vT.
The data structure uses
![]() (n + m) space.
(n + m) space.




