Plane graph copies represent copies of planar graphs or
planarized graphs as planar maps.
| PlaneGraphCopy |
PG |
creates an instance PG of type PlaneGraphCopy initialized
to an empty graph with undefined original graph.
|
| PlaneGraphCopy |
PG(const leda_graph& G, bool preserveMap = true) |
| |
|
creates an instance PG of type PlaneGraphCopy initialized
to a copy of G. If preserveMap is set to false, reversal edges are
considered as multi-edges.
|
| PlaneGraphCopy |
PG(const leda_graph& G, leda_list<leda_edge>& E, bool preserveMap = true) |
| |
|
creates an instance PG of type PlaneGraphCopy initialized
to a copy of G without the edges in E. Precondition: Each e 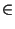 E
is an edge in G. If preserveMap is set to false, reversal edges are
considered as multi-edges. E
is an edge in G. If preserveMap is set to false, reversal edges are
considered as multi-edges.
|
| PlaneGraphCopy |
PG(const PlaneGraphCopy& PG) |
| |
|
creates an instance PG of type PlaneGraphCopy initialized
to a copy of
original(PG).
|
| PlaneGraphCopy |
PG(const PlaneGraphCopy& PG, leda_node_array<leda_node>& v_copy, leda_edge_array<leda_edge>& e_copy) |
| |
|
creates an instance PG of type PlaneGraphCopy initialized
to a copy of
original(PG). Returns in v_copy the newly created
nodes, i.e.,
v copy[v] is the node created for node
v copy[v] is the node created for node
v 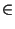 PG,
and in e_copy the newly created edges, i.e.,
e PG,
and in e_copy the newly created edges, i.e.,
e copy[e] is the edge
created for edge
e copy[e] is the edge
created for edge
e 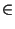 PG. PG.
|
| leda_face |
PG.copy_of_face(leda_face f) |
| |
|
returns a face of PG that corresponds to F.
Precondition: F is a face in G.
|
| leda_edge |
PG.split(leda_edge e) |
split edge e = (v, w) and its reversal r = (w, v) into
edges (v, u), (u, w) and their reversals by introducing a new
node u. Returns the edge (u, w).
|
| leda_edge |
PG.unsplit(leda_node u) |
unsplits a previously split edge e = (v, w), where u
has been created while splitting edge e. Removes u and
inserts edges e' = (v, w) and r = (w, v) according to the embedding.
Returns edge e'.
Precondition: u has exactly two incoming and two outgoing edges,
and has been created by a split operation.
|
| void |
PG.new_edge_chain(leda_edge e, leda_edge from, leda_edge to, const leda_list<leda_edge>& crossings) |
| |
|
Inserts a chain of edges for edge e into PG. Let
crossings = e1,..., ek for a k  0,
ek + 1 = to, and e = (v, w).
Then, we split each ei
(1 < = i < = k) with a node ui,
and insert the
edges
(source(from), u1),
(ui, ui + 1),
(uk, source(to)) into
PG. The inserted edges are appended to chain(e).
Precondition: e is an edge in G, all other edges are edges in PG,
source(from) = copy(v),
source(to) = copy(w),
face(from) = face(e1), and
face(reversal(ei)) = face(ei + 1). 0,
ek + 1 = to, and e = (v, w).
Then, we split each ei
(1 < = i < = k) with a node ui,
and insert the
edges
(source(from), u1),
(ui, ui + 1),
(uk, source(to)) into
PG. The inserted edges are appended to chain(e).
Precondition: e is an edge in G, all other edges are edges in PG,
source(from) = copy(v),
source(to) = copy(w),
face(from) = face(e1), and
face(reversal(ei)) = face(ei + 1).
|
| void |
PG.new_edge_chain(leda_edge e, const leda_list<leda_edge>& crossings) |
| |
|
Inserts a chain of edges for edge e into PG. Let
crossings = e1,..., ek for a k  0,
ek + 1 = to, and e = (v, w).
Then, we split each ei
(1 < = i < = k) with a node ui,
and insert the
edges
(copy(source(e)), u1),
(ui, ui + 1),
(uk, copy(target(e))) into
PG. The inserted edges are appended to chain(e) and a planar
embedding of PG is recomputed.
Precondition: e is an edge in G, all other edges are edges in PG. 0,
ek + 1 = to, and e = (v, w).
Then, we split each ei
(1 < = i < = k) with a node ui,
and insert the
edges
(copy(source(e)), u1),
(ui, ui + 1),
(uk, copy(target(e))) into
PG. The inserted edges are appended to chain(e) and a planar
embedding of PG is recomputed.
Precondition: e is an edge in G, all other edges are edges in PG.
|
| leda_face |
PG.expand(leda_node v) |
replaces node v by a face f. Let
v1,..., vk be the
adjacent nodes of v. Then
f = w1,..., wk, where deg(wi) = 3
and wi is connected to vi. Returns f. Precondition: deg(v) > = 3.
|
| leda_node |
PG.collapse(leda_face f, leda_node v_orig) |
| |
|
collapses face f to a single node v. Sets the original
node of v to v_orig. Serves as undo for expand(v). Returns v.
Precondition: Each node on f has degree 3.
|
| leda_face |
PG.max_face() |
returns a face of PG with maximal degree.
|
| bool |
PG.is_map() |
returns true.
|