Weighted Median Heuristic ( WeightedMedianHeuristic )

Baseclasses

Definition

The class WeightedMedianHeuristic implements the two layer crossing minimization heuristic Weighted-Median. It reorders the nodes on the changeable layer according to the weighted median weight suggested in [GKNV93]

$WeightedMedian(v) = \left\{\begin{array}{cl} 0.0 & \mbox{ if }n=0\\ \frac{1}{... ...2}}) + \ell P(w_{\frac{n}{2}+1})\right) & \mbox{ otherwise} \end{array}\right.$
where $\ell = P(w_{\frac{n}{2}})-P(w_1)$
, $r=P(w_n)-P(w_{\frac{n}{2}+1})$
, v is a node on the changeable layer, and w₁,..., w_n is the sequence of neighbors of v on the fixed layer ordered according to the position P. Thus, the weighted median value of a vertex is defined as the median position of the adjacent vertices if that is uniquely defined. Otherwise, it is interpolated between the two median positions $P(w_{\frac{n}{2}})$
and $P(w_{\frac{n}{2}+1})$
using a measure of tightness. Generally, the weighted median is biased toward the side where vertices are more closely packed.

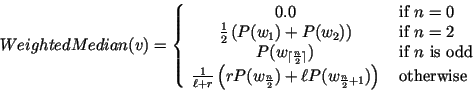
General Information

Algorithm
name	Weighted-Median
long name	Weighted-Median (Gansner et al.)
author	E. R. Gansner, E. Koutsofios, S. C. North, K. P. Vo

Implementation
author	C. Gutwenger
date	Decembre 1998
version	1.0

Pre- and Postcondition

precondition	=	$\emptyset$
postcondition(PRE)	=	$\emptyset$

#include < AGD/WeightedMedianHeuristic.h >

Creation

WeightedMedianHeuristic

M

creates an instance M of type WeightedMedianHeuristic.

Operations

Standard Interface (Inherited Methods) The detailed description of these methods can be found in the manual entries of the base class (TwoLayerCrossMin).

bool	M.check(const leda_graph& G, const Layer& L, AgdKey& p)
void	M.init(const leda_graph& G, const Hierarchy& H)
void	M.call(const leda_graph& G, Layer& L)
void	M.cleanup()

Implementation

We use a randomized quicksort for sorting the nodes on the layer according to the median weight. The init() function takes time $\protectO$(n + m), and the call() function takes expected time $\protectO$(m_L + n_Llogn_L), where n is the number of nodes in the input graph, n_L is the number of nodes on the changeable layer and m_L is the number of edges between the fixed and the changeable layer.