Greedy Switch ( GreedySwitchHeuristic )

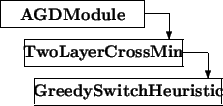
Baseclasses

Definition

The greedy switch heuristic passes over all consecutive pairs of vertices and switches them if this decreases the number of crossings (see Eades and Kelly [EK86]).

General Information

Algorithm
name	Greedy-Switch
long name	Greedy-Switch (Eades,Kelly)
author	P. Eades, D. Kelly

Implementation
author	M. Krüger, Th. Ziegler
date	March 1998
version	1.0

Pre- and Postcondition

precondition	=	$\emptyset$
postcondition(PRE)	=	$\emptyset$

#include < AGD/GreedySwitchHeuristic.h >

Creation

GreedySwitchHeuristic

M

creates an instance M of type GreedySwitchHeuristic.

Operations

Standard Interface (Inherited Methods) The detailed description of these methods can be found in the manual entries of the base class (TwoLayerCrossMin).

bool	M.check(const leda_graph& G, const Layer& L, AgdKey& p)
void	M.init(const leda_graph& G, const Hierarchy& H)
void	M.call(const leda_graph& G, Layer& L)
void	M.cleanup()

Implementation

Let n_L denote the number of nodes on the changeable layer and m_L the number of edges between the fixed and the changeable layer. The algorithm computes in a preprocessing step a so-called crossing matrix, which takes time $\protectO$(n_Lm_L). For the running time of the actual crossing reduction algorithm, we quote the paper: ``The time complexity of this algorithm is hard to compute, because it depends on the number of switchings required to reach a stable ordering. However, since the total number of crossings is at most m², we can at least guarantee that the algorithm is $\protectO$(n_Lm_L²).''