Split Heuristic ( SplitHeuristic )

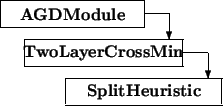
Baseclasses

Definition

The module SplitHeuristic chooses a pivot vertex v and places every other vertex to the left or right of v according to whether it would make fewer crossings. This step is applied recursively to order the left hand side and right hand side of v (see Eades and Kelly [EK86]).

General Information

Algorithm
name	Split
long name	Split (Eades,Kelly)
author	P. Eades, D. Kelly

Implementation
author	M. Krüger, Th. Ziegler
date	March 1998
version	1.0

Pre- and Postcondition

precondition	=	$\emptyset$
postcondition(PRE)	=	$\emptyset$

#include < AGD/SplitHeuristic.h >

Creation

SplitHeuristic

M

creates an instance M of type SplitHeuristic.

Operations

Standard Interface (Inherited Methods) The detailed description of these methods can be found in the manual entries of the base class (TwoLayerCrossMin).

bool	M.check(const leda_graph& G, const Layer& L, AgdKey& p)
void	M.init(const leda_graph& G, const Hierarchy& H)
void	M.call(const leda_graph& G, Layer& L)
void	M.cleanup()

Implementation

Let n_L denote the number of nodes on the changeable layer and m_L the number of edges between the fixed and the changeable layer. The algorithm computes in a preprocessing step a so-called crossing matrix, which takes time $\protectO$(n_Lm_L). The actual crossing reduction algorithm takes time $\protectO$(n_Llogn_L). Both steps are implemented in the call()-method.